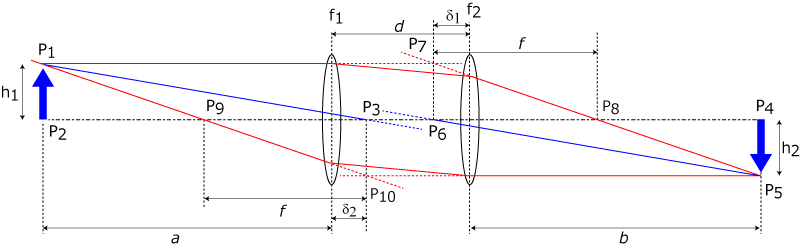
レンズの中心を通る光線の関係

左側の像の先端,P1,から主点,P3,に向かう線と,右側の結像の先端,P5,から主点,P6,に向かう線は平行っぽいですね.
これを証明していきましょう.
そのためには,△P1P2P3と△P4P5P6の相似関係を示せばいいので,
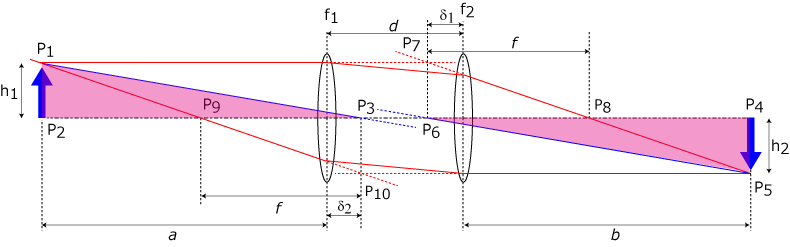
\(\Large \displaystyle \frac{h_1}{a + \delta_2} = \frac{h_2}{b + \delta_1} \)
であることを証明すればよいわけです. △P4P5P8と△P6P7P8の関係から,
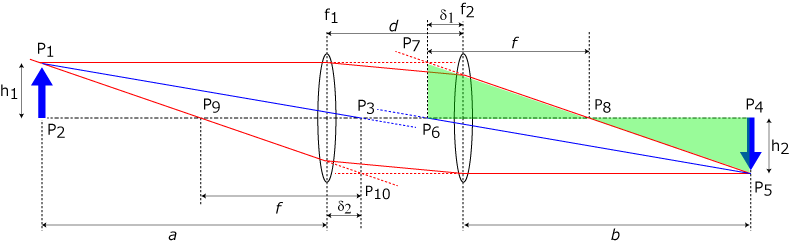
\(\Large \displaystyle \frac{h_1}{f} = \frac{h_2}{b + \delta_1 - f } \)
△P1P2P9と△P10P3P9の関係から,
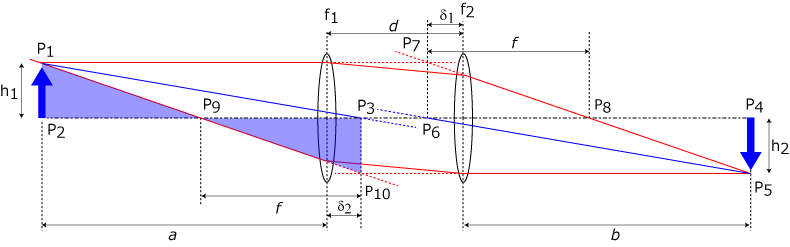
\(\Large \displaystyle \frac{h_1}{a + \delta_2 - f} = \frac{h_2}{ f } \)
を得ることができます.ここで,f,を消去すると,
\(\Large \displaystyle h_1 (b + \delta_1 - f) = h_2 f \)
\(\Large \displaystyle h_1 (b + \delta_1 ) = (h_1 + h_2) f \)
\(\Large \displaystyle h_1 f = h_2 (a + \delta_2 - f) \)
\(\Large \displaystyle (h_1 + h_2) f = h_2 (a + \delta_2 ) \)
となるので,
\(\Large \displaystyle h_1 (b + \delta_1 ) = h_2 (a + \delta_2 ) \)
\(\Large \displaystyle \frac{h_1}{a + \delta_2} = \frac{h_2}{b + \delta_1 } \)
を満たすことができたので,二つの線(図の中の青い線)は,平行であることがわかります.
では,次にレンズの公式,倍率を求めていきましょう.